Parsing Expression

Grammar rules

Ở phần trước, chúng ta biết rằng expression trong Lox có thể được generate theo những quy tắc sau

expression     → literal
               | unary
               | binary
               | grouping ;

literal        → NUMBER | STRING | "true" | "false" | "nil" ;
grouping       → "(" expression ")" ;
unary          → ( "-" | "!" ) expression ;
binary         → expression operator expression ;
operator       → "==" | "!=" | "<" | "<=" | ">" | ">="
               | "+"  | "-"  | "*" | "/" ;

Xét biểu thức:

Sử dụng quy tắc trên, có hai cách để generate ra biểu thức này, và cho ra hai kết quả khác nhau!

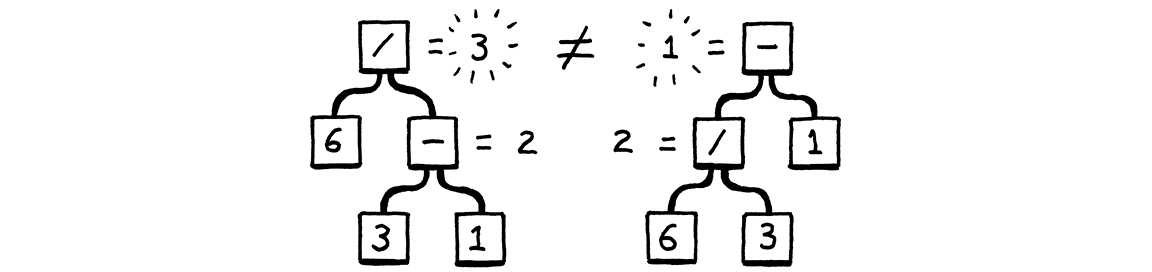
Như vậy quy tắc grammar trên có sự mơ hồ (ambiguity). Trong toán học, vấn đề này được giải quyết bằng 2 luật

• Precedence: quy định phép toán được tính trước trong một biểu thức gồm nhiều loại phép toán. E.g: phép nhân (x) được tính trước phép cộng (+).

  Precedence, lowest to highest
  | =
  | or
  | and
  | ==, !=
  | <, >, <=, >=
  | +, -
  | *, /
  | not, - (negate)
  v ()

• Associativity: quy định toán tử được tính trước trong một biểu thức gồm nhiều toán tử giống nhau.

  • Phép cộng là left-associate. E.g: 1 + 2 + 3 có thể viết dưới dạng (1 + 2) + 3
  • Phép gán (=) là right-associate. E.g: x = y = z có thể viết dưới dạng x = (y = z)

| Name        | Operator     | Associativity |
| --------    | --------     | -------- |
| Equality    | ==, !=       | Left     |
| Comparison  | >, >=, <, <= | Left     |
| Term        | +, -         | Left     |
| Factor      | * /          | Left     |
| Unary       | !, -         | Right    |

Dựa vào luật precedence và associativity, ta có thể viết lại ngữ pháp cho expression nhằm loại bỏ sự mơ hồ của ngữ pháp ở phần trước:

expression     → equality ;
equality       → comparison ( ( "!=" | "==" ) comparison )* ;
comparison     → term ( ( ">" | ">=" | "<" | "<=" ) term )* ;
term           → factor ( ( "-" | "+" ) factor )* ;
factor         → unary ( ( "/" | "*" ) unary )* ;
unary          → ( "!" | "-" ) unary
               | primary ;
primary        → NUMBER | STRING | "true" | "false" | "nil"
               | "(" expression ")" ;

Dưới đây, parser sẽ được cài đặt theo ngữ pháp này.

Expression parser

Trong phần này, ta sử dụng kĩ thuật parsing có tên Recursive Descent Parsing. Kĩ thuật này có cách tiếp cận top-down, tức là bắt đầu từ rule trên cùng (expression) và dần dần đi xuống từng tầng cho đến rule cuối cùng (primary).

Parse function

  // Parse a single expression and return remaining tokens
  def parse(ts: List[Token]): ParseResult = expression(ts)

  def expression(tokens: List[Token]): ParseResult = equality(tokens)

Parse function trả ra một expression hoàn chỉnh và tokens còn lại sau quá trình parse.

Mỗi rule (e.g: expression, equality, etc) sẽ tương ứng với một hàm và có kiểu input/output tương tự hàm parse.

Binary expression

Hãy bắt đầu với ví dụ:

Parse biểu thức a * b + c - d

Biểu thức trên được viết dưới dạng tokens như sau

| a | * | b | + | c | - | d | ; |

Rule được sử dụng để parse là

term           → factor ( ( "-" | "+" ) factor )* ;

Các bước trong quá trình parse sẽ diễn ra như sau

Step	Description	Expr	Remaining tokens
0	Khởi đầu	(?)	a * b + c - d ;
1	Chạy rule factor(a * b + c - d ;)	a * b	+ c - d ;
2	Thêm dấu +	a * b + (?)	c - d ;
3	Chạy rule factor(c - d ;)	a * b + c	- d ;
4	Thêm dấu -	a * b + c - (?)	d ;
5	Chạy rule factor(d ;)	a * b + c - d	;
6	Kết thúc	a * b + c - d	;

Mặc dù ví dụ ở trên giải thích các bước parse phép cộng (term), nhưng ta hoàn toàn có thể áp dụng thuật toán này cho các phép toán nhị phân (binary expression) khác.

Trong Scala, thuật toán trên được cài đặt như sau:

  def binary(
    op: BinaryOp,
    descendant: List[Token] => ParseResult,
  )(
    tokens: List[Token]
  ): ParseResult =
    def matchOp(ts: List[Token], l: Expr): ParseResult =
      ts match
        case token :: rest =>
          op(token) match
            case Some(fn) => descendant(rest).flatMap((r, rmn) => matchOp(rmn, fn(l, r)))
            case None     => Right(l, ts)
        case _ => Right(l, ts)

    descendant(tokens).flatMap((expr, rest) => matchOp(rest, expr))

sau đó có thể sử dụng hàm này này cho các phép toán nhị phân

  def equality = binary(equalityOp, comparison)
  def comparison = binary(comparisonOp, term)
  def term = binary(termOp, factor)
  def factor = binary(factorOp, unary)

Unary expression

Lưu ý, unary là right-associate operator, vì thế ta gọi đệ quy hàm unary ngay khi gặp dấu ! hoặc -. Nếu không gặp một trong hai dấu trên, ta gọi xuống hàm primary.

  def unary(tokens: List[Token]): ParseResult =
    tokens match
      case token :: rest =>
        unaryOp(token) match
          case Some(fn) => unary(rest).flatMap((expr, rmn) => Right(fn(expr), rmn))
          case None     => primary(tokens)
      case _ => primary(tokens)

Primary expression

Cài đặt primary expression tương đối rõ ràng

  def primary(tokens: List[Token]): ParseResult =
    tokens match
      case Literal.Number(l) :: rest  => Right(Expr.Literal(l.toDouble), rest)
      case Literal.Str(l) :: rest     => Right(Expr.Literal(l), rest)
      case Keyword.True :: rest       => Right(Expr.Literal(true), rest)
      case Keyword.False :: rest      => Right(Expr.Literal(false), rest)
      case Keyword.Nil :: rest        => Right(Expr.Literal(null), rest)
      case Operator.LeftParen :: rest => parenBody(rest)
      case _                          => Left(Error.ExpectExpression(tokens))

Khi gặp dấu mở ngoặc (left paren), ta tiếp tục chạy rule expression cho những tokens tiếp theo, sau đó kiểm tra token kế tiếp có phải dấu đóng ngoặc hay không.

  def parenBody(
    tokens: List[Token]
  ): ParseResult = expression(tokens).flatMap((expr, rest) =>
    rest match
      case Operator.RightParen :: rmn => Right(Expr.Grouping(expr), rmn)
      case _                          => Left(Error.ExpectClosing(rest))
  )