Representing Code

Ở phần trước, chúng ta đã thử biến đổi source code từ dạng raw sang một list tokens. Hôm nay, chúng ta sẽ tiếp tục biểu diễn list token này sang 1 dạng phức tạp và đầy đủ hơn.

Đầu tiên, chúng ta sẽ bắt đầu với 1 ví dụ đơn giản, làm thế nào để tính biểu thức sau:

1 + 2 * 3 - 4

Chúng ta đều biết quy tắc giải bài toán này đó là "nhân chia trước, cộng trừ sau". Trên máy tính, nó có thể được biểu diễn bằng cấu trúc cây. Trong đó, số là các node lá và toán tử là các node trong.

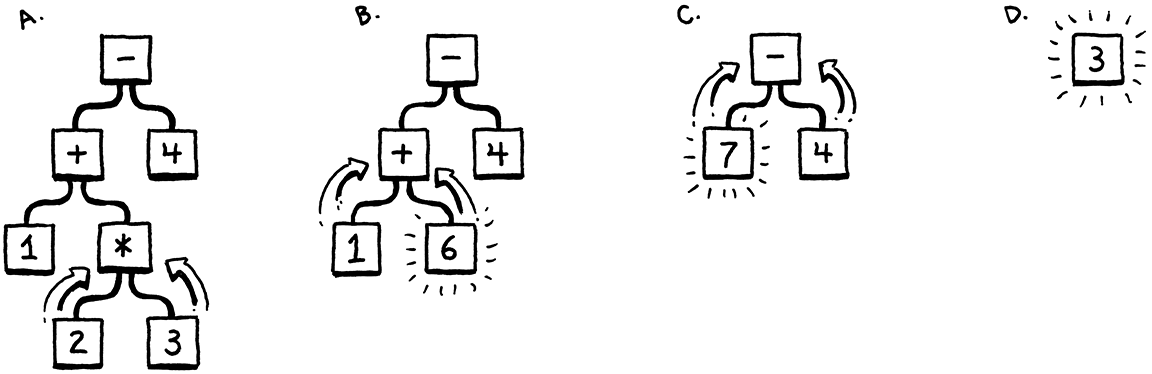
Để tính được giá trị của biểu thức, chúng ta sẽ phải tính giá trị của các cây con trước. Tức là chúng ta phải thực hiện duyệt cây (tree traversal), trong ví dụ này chúng ta sẽ thực hiện post-order traversal.

Chúng ta thấy là nếu dùng cấu trúc cây để biểu diễn biểu thức trên thì việc tính toán trông khá dễ dàng. Vậy 1 cách trực quan nhất, liệu chúng ta có thể biểu diễn grammar của ngôn ngữ lập trình dưới dạng dạng cây hay không?

Context-Free Grammars

Ở bài trước, chúng ta cũng đã sử dụng lexical grammar để định nghĩa các tokens. Với Scanner thì cách làm này rất hiệu quả nhưng không đủ để handle các biểu thức lồng nhau rất phức tạp.

Vì vậy, chúng ta sẽ cần đến context-free grammar (CFG). Công cụ mạnh nhất trong các ngôn ngữ hình thức

Một ngôn ngữ hình thức (formal language) được định nghĩa là một tập các chuỗi (string) được xây dựng dựa trên một bảng chữ cái (alphabet), và chúng được ràng buộc bởi các luật (rule) hoặc văn phạm (grammar) đã được định nghĩa trước.
Wikipedia

Bảng chữ cái ở đây có thể lấy từ ngôn ngữ tự nhiên hoặc tự định nghĩa

Terminology		Lexical grammar	Syntactic grammar
The “alphabet” is . . .	→	Characters	Tokens
A “string” is . . .	→	Lexeme or token	Expression
It’s implemented by the . . .	→	Scanner	Parser

Rules for grammars

Chúng ta cần phải định nghĩa một tập giới hạn các quy tắc (rule) để tạo ra các strings. Rules trong trường hợp này gọi là productions vì chúng produce ra các strings.

Mỗi production(rule) trong CFG có phần đầu (head) - tên và phần thân (body) mô tả nó sẽ tạo ra cái gì. Ở dạng cơ bản nhất thì, phần thân chỉ bao gồm một danh sách các kí hiệu (Symbols). Các kí hiệu có 2 kiểu:

Terminal là một chữ cái trong bảng chữ cái. Chúng ta có thể nghĩ nó như là một literal. Trong syntactic grammar nó là các token chúng ta đã có được từ Scanner.
Nonterminal dùng để chỉ đến 1 rule trong gammar.

Chỉ còn 1 điều cuối cùng cần phải lưu ý: Chúng ta có thể có nhiều rules có cùng tên. Khi chúng ta gặp một nonterminal với 1 tên nào đó chúng ta được phép chọn 1 rule bất kì cho nó.

Để biểu diễn được 1 cách cụ thể hơn, chúng ta cần một cách để viết ra các production rules này. Người ta đã tìm cách thực hiện điều này từ hàng ngàn năm về trước và cho đến khi John Backus và công ty của ông cần nó cho ngôn ngữ ALGOL 58 và cuối cùng tạo ra Backus-Naur form (BNF). Và kể từ đó, hầu hết mọi người để sử dụng BNF (hoặc biến đổi của BNF).

breakfast  → protein "with" breakfast "on the side" ;
breakfast  → protein ;
breakfast  → bread ;

protein    → crispiness "crispy" "bacon" ;
protein    → "sausage" ;
protein    → cooked "eggs" ;

crispiness → "really" ;
crispiness → "really" crispiness ;

cooked     → "scrambled" ;
cooked     → "poached" ;
cooked     → "fried" ;

bread      → "toast" ;
bread      → "biscuits" ;
bread      → "English muffin" ;

Từ đó chúng ta có thể viết ra các strings dựa trên BNF ở trên:

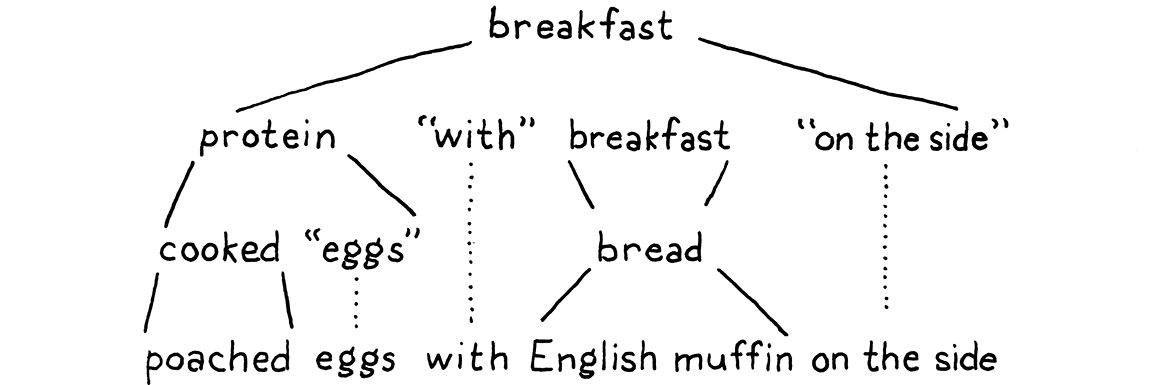
A Grammar for Lox expressions

Syntatic Grammar phức tạp hơn Lexical Grammar rất là nhiều, vì vậy rất khó để trình bày được toàn bộ SG trong 1 lần giống như cách chúng ta làm ở phần Scanner. Vì vậy, chúng ta sẽ nghiền ngẫm từng tập con của ngôn ngữ và thêm syntax mới trong các chương tiếp theo. Hiện tại, chúng ta sẽ chỉ quan tâm đến expression:

expression     → literal
               | unary
               | binary
               | grouping ;

literal        → NUMBER | STRING | "true" | "false" | "nil" ;
grouping       → "(" expression ")" ;
unary          → ( "-" | "!" ) expression ;
binary         → expression operator expression ;
operator       → "==" | "!=" | "<" | "<=" | ">" | ">="
               | "+"  | "-"  | "*" | "/" ;

Trên đây là các rule để chúng ta có thể biểu diễn được 1 expression giống như sau:

1 - (2 * 3) < 4 == false

Implementing Syntax Trees

Dễ thấy, grammar của chúng ta có thể được biểu diễn bằng cấu trúc cây. Bởi vì cấu trúc này được dùng để biểu diễn syntax cho ngôn ngữ grox nên nó được gọi là syntax tree.

Modelling Data with Algebraic Data Type

Trong FP, ADT là một kiểu dữ liệu được tạo nên bằng cách kết hợp các kiểu dữ liệu khác.

Ví dụ 1: 1 biểu thức Binary sẽ có vế trái, về phái và 1 toán tử. Trong Scala chúng ta có thể biểu diễn kiểu Binary bằng 1 case class:

case class Binary(left: Expr, operator: Operator, right: Expr)

Khi đó, Binary được gọi là 1 Product Type

Ví dụ 2: 1 Literal có thể là Number hoặc String. Với Scala chúng ta có thể biểu diễu Literal bằng Enum hoặc Union Type

type Literal = Str | Number
enum Literal:
  case Str, Number

Khi đó, Literal được gọi là 1 Sum type

Trong Scala 3, khái niệm enum để rộng để có thể biểu diễn luôn một ADT hoàn chỉnh hay thậm chí là một Generalize ADT (GADT).

Ví dụ chúng ta có thể định nghĩa expression của grammar trên trong Scala 3 như sau:

enum Expr:
  case Binary(left: Expr, o: Operator, right: Expr)
  case Unary(o: Operator, expr: Expr)
  case Grouping(expr: Expr)
  case Literal(o: Str | Number)

Tuy nhiên ở chương này, chúng ta sẽ define Expr một cách tường minh hơn bằng cách tách biệt Binary thành các phép toán số học như bên dưới:

enum Expr:
  case Add(left: Expr, right: Expr)
  case Subtract(left: Expr, right: Expr)
  case Multiply(left: Expr, right: Expr)
  case Divide(left: Expr, right: Expr)
  case Negate(expr: Expr)
  case Minus(expr: Expr)
  case Number(value: Int | Double)
  case Str(value: String)
  case Grouping(expr: Expr)

Để đơn giản, trong chương này chúng ta sẽ quan tâm đến một số phép tính số học, trong các phần sau chúng ta sẽ tìm hiểu thêm về các biểu thức logic.

Working with Trees

OOP vs FP

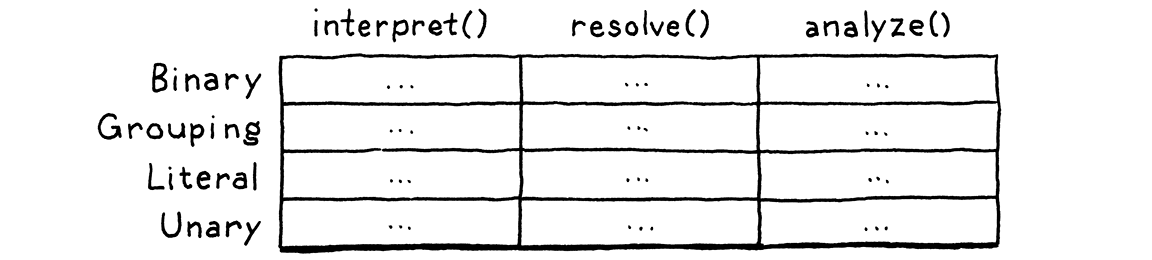
Chúng ta thấy rằng, với mỗi kiểu expression chúng ta sẽ có 1 số các operations đi kèm với nó.

Trong các ngôn ngữ OOP như Java, code của chúng ta thường sẽ theo hướng là các ô trên cùng 1 hàng sẽ dính liền với nhau. Tức là các kiểu expression sẽ share chung với nhau các operation.

Vì vậy, khi chúng ta thêm 1 kiểu expression mới, thì code của chúng ta sẽ rất đơn giản. Chúng ta không cần phải động vào các kiểu expression đã có mà chỉ cần "extends" thêm 1 kiểu mới. Nhưng khi chúng ta muốn thêm 1 operation mới, thì chúng ta phải quay lại và sửa lại tất cả các expression đã có.

Đối với các ngôn ngữ FP như ML. Type và Operation tách biệt nhau, mỗi kiểu expression khác nhau thì chúng có các operation khác nhau cho kiểu đó. Vì vậy, các ô trong cùng 1 cột sẽ dính liền với nhau.

Trong FP, khi chúng ta muốn định nghĩa 1 function cho nhiều kiểu expression khác nhau. Chúng ta sẽ dùng đến pattern matching. Khi chúng ta thêm 1 operation mới, chúng ta sẽ không cần sửa các operation khác. Tuy nhiên, khi chúng ta có thêm 1 kiểu mới, chúng ta phải quay lại và sửa code của tất cả các operation đã có.

A (Not Very) Pretty Printer

Khi chúng ta debug parser, chúng ta thường phải debug AST. Vì vậy chúng ta muốn có 1 format đẹp cho AST. Quá trình convert 1 AST sang string thường được gọi là "pretty printing".

Thế nhưng, 1 printer không nên in ra những cái kiểu như 1 + 2 * 3 mà để phục vụ debug, chúng ta cần phải biểu diễn xem là phép toán nào đươc thực hiện trước, phép + hay phép * là đỉnh của cây.

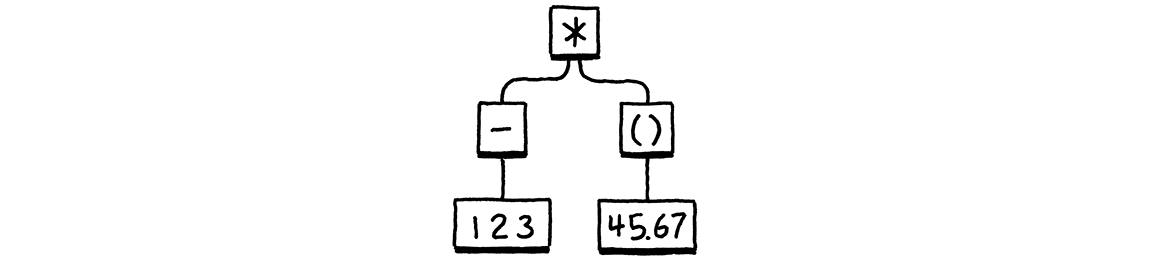
AST ở trên sẽ được in ra là (xem sourcecode):

(* (- 123) (group 45.67))

Representing Code

Context-Free Grammars​

Rules for grammars​

A Grammar for Lox expressions​

Implementing Syntax Trees​

Modelling Data with Algebraic Data Type​

Working with Trees​

A (Not Very) Pretty Printer​